Определение. Особая точка функции называется изолированной, если в некоторой окрестности этой точки - аналитическая функция (то есть аналитическая в кольце ).
Классификация изолированных особых точек функции связана с поведением этой функции в окрестности особой точки.
Определение. Точка называется устранимой особой точкой функции , если существует конечный предел этой функции при .
Пример 5. Показать, что функция имеет в точке устранимую особенность.
Решение. Вспоминая первый замечательный предел, вычислим
Значит, в точке заданная функция имеет устранимую особенность.
Задача 4. Показать, что точка устранимая для .
Определение. Точка называется полюсом функции , если эта функция неограниченно возрастает при , то есть .
Обратим внимание на связь между понятиями нуля и полюса аналитической функции. Представим функцию в виде .
Если точка является простым нулем функции , то функция имеет в простой полюс
Если точка - нуль порядка для функции , то для функции это полюс порядка .
Пример 6. Показать, что функция имеет в точке полюс третьего порядка.
Решение. Полагая , получим . При стремлении к нулю по любому закону имеем . Тогда , а с ним и сама функция неограниченно возрастает. Следовательно, , то есть особая точка является полюсом. Для функции эта точка, очевидно, является трехкратным нулем. Значит, для данной функции точка является полюсом третьего порядка.
Задача 5. Показать, что в точке имеет простой полюс.
Определение. Точка называется существенно особой точкой функции , если в этой точке не существует ни конечного, ни бесконечного предела функции (поведение функции не определено).
Пусть является существенно особой точкой функции . Тогда для любого наперед заданного комплексного числа найдется такая последовательность точек , сходящаяся к , вдоль которой значения стремятся к : (теорема Сохоцкого).
Пример 7. Показать, что функция в точке имеет существенную особенность.
Решение. Рассмотрим поведение заданной функции в окрестности точки . При вдоль положительной части действительной оси (т.е. ) имеем и ; если же вдоль отрицательной части действительной оси (т.е. ), то и . Значит, не существует предела при . По определению, в точке функция имеет существенную особенность.
Рассмотрим поведение функции в нуле с точки зрения теоремы Сохоцкого. Пусть - любое комплексное число, отличное от нуля и бесконечности.
Из равенства находим . Полагая , получим последовательность точек , . Очевидно, . В каждой точке этой последовательности функция равна , поэтому и
Задача 6. Показать, что функция имеет в точке существенную особенность.
Бесконечно удаленная точка всегда считается особой для функции . Точка называется изолированной особой точкой функции , если эта функция вне некоторого круга с центром в начале координат не имеет других особых точек.
Классификацию изолированных особых точек можно распространить и на случай .
Пример 8. Показать, что функция имеет на бесконечности двукратный полюс.
Решение. Рассмотрим функцию , где - аналитическая функция в окрестности точки , причем . Значит, функция имеет на бесконечности двукратный нуль, но тогда для функции точка является двукратным полюсом.
Пример 9. Показать, что функция имеет на бесконечности существенную особенность.
Решение. Аналогичная задача рассмотрена в пр.7. Рассмотрим поведение функции в окрестности бесконечно удаленной точки. При вдоль положительной части действительной оси , а при вдоль отрицательной части действительной оси . Значит, не существует предела функции в точке и в силу определения эта точка - существенно особая.
О характере особенности функции в точке можно судить по главной части лорановского разложения в окрестности этой точки.
Теорема 1. Для того чтобы точка была устранимой особой точкой функции , необходимо и достаточно, чтобы соответствующее лорановское разложение не содержало главной части.
Задача 6. Пользуясь тейлоровским разложением функции в окрестности точки , показать, что имеет в нуле устранимую особенность.
Теорема 2. Для того чтобы точка была полюсом функции , необходимо и достаточно, чтобы главная часть соответствующего лорановского разложения содержала конечное число членов :
Номер старшего отрицательного члена определяет порядок полюса.
В этом случае функцию можно представить в виде
где - аналитическая в точке функция, , - порядок полюса.
Пример 10. Показать, что функция имеет в точках и простые полюсы.
Решение. Рассмотрим точку . Воспользуемся лорановским разложением данной функции в окрестности этой точки, полученным в примере 2:
Так как в главной части этого разложения старшая (и единственная) отрицательная степень равна единице, то точка - простой полюс данной функции.
Можно было получить этот результат другим путем. Представим в виде и положим - это функция, аналитическая в точке и . Значит, и в силу (8) в точке данная функция имеет простой полюс.
Еще один способ: рассмотрим функцию , которая в точке имеет простой нуль. Значит, в этой точке имеет простой полюс.
Аналогично, если записать функцию в виде , где - функция, аналитическая в точке и , то сразу ясно, что точка - простой полюс функции .
Задача 7. Показать, что функция имеет полюс 2 -го порядка в точке и полюс 4 -го порядка в точке .
Теорема 3. Для того чтобы точка была существенно особой точкой функции , необходимо и достаточно, чтобы главная часть лорановского разложения в окрестности точки содержала бесконечное число членов .
Пример 11. Определить характер особенности в точке функции
Решение. В известном разложении косинуса положим вместо :
Значит, лорановское разложение в окрестности точки имеет вид
Здесь правильная часть - одно слагаемое . А главная часть содержит бесконечное число слагаемых, поэтому точка - существенно особая.
Задача 8. Показать, что в точке функция имеет существенную особенность.
Рассмотрим некоторую функцию и запишем ее лорановское разложение в точке :
Произведем замену , при этом точка переходит в точку . Теперь в окрестности бесконечно удаленной точки имеем
Осталось ввести новое обозначение . Получаем
где - главная часть, а - правильная часть лорановского разложения функции в окрестности бесконечно удаленной точки. Таким образом, в лорановском разложении функции в окрестности точки главная часть - это ряд по положительным степеням , а правильная часть - ряд по отрицательным степеням. С учетом этого заме
чания приведенные критерии для определения характера особенности остаются в силе и для бесконечно удаленной точки.
Пример 12. Выяснить характер особенности функции в точке . , то в точке может оказаться неизолированной.
Пример 15. Функция в бесконечно удаленной точке имеет существенную особенность. Показать, что точка для функции не является изолированной особой точкой.
Решение. Функция имеет бесчисленное множество полюсов в нулях знаменателя, то есть в точках , . Так как , то точка , в любой окрестности которой имеются полюсы , является предельной для полюсов.
Модели, описываемые системами двух автономных дифференциальных уравнений.
Фазовая плоскость. Фазовый портрет. Метод изоклин. Главные изоклины. Устойчивость стационарного состояния. Линейные системы. Типы особых точек: узел, седло, фокус, центр. Пример: химические реакции первого порядка.
Наиболее интересные результаты по качественному моделированию свойств биологических систем получены на моделях из двух дифференциальных уравнений, которые допускают качественное исследование с помощью метода фазовой плоскости . Рассмотрим систему двух автономных обыкновенных дифференциальных уравнений общего вида
(4.1)
P(x,y), Q(x,y) - непрерывные функции, определенные в некоторой области G евклидовой плоскости (x,y ‑ декартовы координаты) и имеющие в этой области непрерывные производные порядка не ниже первого.
Область G может быть как неограниченной, так и ограниченной. Если переменные x, y имеют конкретный биологический смысл (концентрации веществ, численности видов) чаще всего область G представляет собой положительный квадрант правой полуплоскости:
0 £ x< ¥ ,0 £ y < ¥ .
Концентрации веществ или численности видов также могут быть ограничены сверху объемом сосуда или площадью ареала обитания. Тогда область значений переменных имеет вид:
0 £ x < x 0 , 0 £ y< y 0 .
Переменныеx, y во времени изменяются в соответствии с системой уравнений (4.1), так что каждому состоянию системы соответствует пара значений переменных (x, y ).
|
|
Обратно, каждой паре переменных (x, y ) соответствует определенное состояние системы.
Рассмотрим плоскость с осями координат, на которых отложены значения переменных x,y . Каждая точка М этой плоскости соответствует определенному состоянию системы. Такая плоскость носит название фазовой плоскости и изображает совокупность всех состояний системы. Точка М(x,y)называется изображающей или представляющей точкой.
Пусть в начальный момент времени t=t 0 координаты изображающей точки М 0 (x (t 0), y (t 0)). В каждый следующий момент времени t изображающая точка будет смещаться в соответствии с изменениями значений переменных x (t ), y (t ). Совокупность точек М (x (t ), y(t )) на фазовой плоскости, положение которых соответствует состояниям системы в процессе изменения во времени переменных x(t) , y(t) согласно уравнениям (4.1), называется фазовой траекторией.
Совокупность фазовых траекторий при различных начальных значениях переменных дает легко обозримый "портрет" системы. Построение фазового портрета позволяет сделать выводы о характере изменений переменных x, y без знания аналитических решений исходной системы уравнений (4.1).
Для изображения фазового портрета необходимо построить векторное поле направлений траекторий системы в каждой точке фазовой плоскости. Задавая приращение D t>0, получим соответствующие приращения D x и D y из выражений:
D x=P(x,y) D t ,
D y=Q(x,y) D t.
Направление вектора dy/dx в точке (x, y ) зависит от знака функций P(x, y), Q(x, y) и может быть задано таблицей:
|
P(x,y)>0,Q(x,y)>0 |
|
|
P(x,y)<0,Q(x,y)<0 |
|
|
P(x,y)>0,Q(x,y)<0 |
|
|
P(x,y)<0,Q(x,y)>0 |
|
.(4.2)
Решение этого уравнения y = y (x, c ), или в неявном виде F (x,y )=c, где с – постоянная интегрирования, дает семейство интегральных кривых уравнения (4.2) ‑ фазовых траекторий системы (4.1) на плоскости x, y .
Метод изоклин
Для построения фазового портрета пользуются методом изоклин – на фазовой плоскости наносят линии, которые пересекают интегральные кривые под одним определенным углом. Уравнение изоклин легко получить из (4.2). Положим
где А – определенная постоянная величина. Значение А представляет собой тангенс угла наклона касательной к фазовой траектории и может принимать значения от – ¥ до + ¥ . Подставляя вместо dy/dx в (4.2) величину А получим уравнение изоклин:
.(4.3)
Уравнение (4.3) определяет в каждой точке плоскости единственную касательную к соответствующей интегральной кривой за исключением точки, где P (x,y ) = 0, Q (x,y ) = 0 , в которой направление касательной становится неопределенным, так как при этом становится неопределенным значение производной:
.
Эта точка является точкой пересечения всех изоклин – особой точкой. В ней одновременно обращаются в нуль производные по времени переменных x и y .
Таким образом, в особой точке скорости изменения переменных равны нулю. Следовательно, особая точка дифференциальных уравнений фазовых траекторий (4.2) соответствует стационарному состоянию системы (4.1),а ее координаты – суть стационарные значения переменных x, y.
Особый интерес представляют главные изоклины:
dy/dx=0, P (x,y )=0 – изоклина горизонтальных касательных и
dy/dx= ¥ , Q (x,y )=0 – изоклина вертикальных касательных.
Построив главные изоклины и найдя точку их пересечения (x,y ), координаты которой удовлетворяют условиям:
мы найдем тем самым точку пересечения всех изоклин фазовой плоскости, в которой направление касательных к фазовым траекториям неопределенно. Это – особая точка , которая соответствует стационарному состоянию системы (рис. 4.2).
Система (4.1) обладает столькими стационарными состояниями, сколько точек пересечения главных изоклин имеется на фазовой плоскости.
Каждая фазовая траектория соответствует совокупности движений динамической системы, проходящих через одни и те же состояния и отличающихся друг от друга только началом отсчета времени.
 |
|
Если условия теоремы Коши выполнены, то через каждую точку пространства x, y, t проходит единственная интегральная кривая. То же справедливо, благодаря автономности, для фазовых траекторий: через каждую точку фазовой плоскости проходит единственная фазовая траектория.
Устойчивость стационарного состояния
Пусть система находится в состоянии равновесия.
Тогда изображающая точка находится в одной из особых точек системы, в которых по определению:
.
Устойчива или нет особая точка, определяется тем, уйдет или нет изображающая точка при малом отклонении от стационарного состояния. Применительно к системе из двух уравнений определение устойчивости на языке e , d выглядит следующим образом.
Состояние равновесия устойчиво, если для любой заданной области отклонений от состояния равновесия (e ) можно указать область d (e ), окружающую состояние равновесия и обладающую тем свойством, что ни одна траектория, которая начинается внутри области d , никогда не достигнет границы e . (рис. 4.4)
 |
|
Для большого класса систем – грубых систем – характер поведения которых не меняется при малом изменении вида уравнений, информацию о типе поведения в окрестности стационарного состояния можно получить, исследуя не исходную, а упрощенную линеаризованную систему.
Линейные системы.
Рассмотрим систему двух линейных уравнений:
.(4.4)
Здесь a, b, c, d - константы, x, y ‑ декартовы координаты на фазовой плоскости.
Общее решение будем искать в виде:
.(4.5)
Подставимэти выражения в (4.4) и сократим на e l t :
(4.6)
Алгебраическая система уравнений (4.6) с неизвестными A, B имеет ненулевое решение лишь в том случае, если ее определитель, составленный из коэффициентов при неизвестных, равен нулю:
.
Раскрывая этот определитель, получим характеристическое уравнение системы:
.(4.7)
Решение этого уравнения дает значения показателя l 1,2 , при которых возможны ненулевые для A и B решения уравнения (4.6). Эти значения суть
.(4.8)
Если подкоренное выражение отрицательно, то l 1,2 комплексно сопряженные числа. Предположим, что оба корня уравнения (4.7) имеют отличные от нуля действительные части и что нет кратных корней. Тогда общее решение системы (4.4) можно представить в виде линейной комбинации экспонент с показателями l 1 , l 2 :
(4.9)
Для анализа характера возможных траекторий системы на фазовой плоскости используем линейное однородное преобразование координат, которое позволит привести систему к каноническому виду:
,(4.10)
допускающее более удобное представление на фазовой плоскости по сравнению с исходной системой (4.4). Введем новые координаты ξ , η по формулам:
(4.1)
Из курса линейной алгебры известно, что в случае неравенства нулю действительных частей l 1 , l 2 исходную систему (4.4) при помощи преобразований (4.11) всегда можно преобразовать к каноническому виду (4.10) и изучать ее поведение на фазовой плоскости ξ , η . Рассмотрим различные случаи, которые могут здесь представиться.
Корни λ 1 , λ 2 – действительны и одного знака
В этом случае коэффициенты преобразования действительны, мы переходим от действительной плоскости x,y к действительной плоскости ξ, η. Разделив второе из уравнений (4.10) на первое, получим :
.(4.12)
Интегрируя это уравнение, находим :
Где .(4.13)
Условимся понимать под λ 2 корень характеристического уравнения с большим модулем, что не нарушает общности нашего рассуждения. Тогда, поскольку в рассматриваемом случае корни λ 1 , λ 2 – действительны и одного знака, a >1 , и мы имеем дело с интегральными кривыми параболического типа.
Все интегральные кривые (кроме оси η , которой соответствует ) касаются в начале координат оси ξ, которая также является интегральной кривой уравнения (4.11). Начало координат является особой точкой.
Выясним теперь направление движений изображающей точки вдоль фазовых траекторий. Если λ 1 , λ 2 – отрицательны, то, как видно из уравнений (4.10), |ξ|, |η| убывают с течением времени. Изображающая точка приближается к началу координат, никогда, однако, не достигая его. В противном случае это противоречило бы теореме Коши, которая утверждает, что через каждую точку фазовой плоскости проходит лишь одна фазовая траектория.
Такая особая точка, через которую проходят интегральные
кривые, подобно тому, как семейство парабол
проходит через
начало координат, носит название узла(рис.
4.5)
Состояние равновесия типа узел при λ 1 , λ 2 < 0 устойчиво по Ляпунову, так как изображающая точка по всем интегральным кривым движется по направлению к началу координат. Это устойчивый узел . Если же λ 1 , λ 2 > 0, то |ξ|, |η| возрастают с течением времени и изображающая точка удаляется от начала координат. В этом случае особая точка – неустойчивый узел .
На фазовой плоскости x, y общий качественный характер поведения интегральных кривых сохранится, но касательные к интегральным кривым не будут совпадать с осями координат. Угол наклона этих касательных будет определяться соотношением коэффициентов α , β , γ , δ в уравнениях (4.11).
Корни λ 1 , λ 2 – действительны и разных знаков.
Преобразование от координат x,y к координатам ξ, η опять действительное. Уравнения для канонических переменных снова имеют вид (4.10), но теперь знаки λ 1 , λ 2 различны. Уравнение фазовых траекторий имеет вид :
Где ,(4.14)
Интегрируя (4.14), находим
(4.15)
Это уравнение определяет семейство кривых гиперболического типа, где обе оси координат – асимптоты (при a =1 мы имели бы семейство равнобочных гипербол) . Оси координат и в этом случае являются интегральными кривыми – это будут единственные интегральные кривые, проходящие через начало координат. Каждая из них состоит из трех фазовых траекторий : из двух движений к состоянию равновесия (или от состояния равновесия) и из состояния равновесия. Все остальные интегральные кривые – суть гиперболы, не проходящие через начало координат (рис. 4.6) Такая особая точка носит название «седло ». Линии уровня вблизи горной седловины ведут себя подобно фазовым траекториям в окрестности седла.
Рассмотрим характер движения изображающей точки по фазовым траекториям вблизи состояния равновесия. Пусть, например, λ 1 >0 , λ 2 <0 . Тогда изображающая точка, помещенная на оси ξ , будет удаляться от начала координат, а помещенная на оси η – будет неограниченно приближаться к началу координат , не достигая его за конечное время . Где бы ни находилась изображающая точка в начальный момент (за исключением особой точки и точек на асимптоте η =0), она в конечном счете будет удаляться от состояния равновесия, даже если в начале она движется по одной из интегральных кривых по направлению к особой точке .
Очевидно, что особая точка типа седла всегда неустойчива . Только при специально выбранных начальных условиях на асимптоте η =0 система будет приближаться к состоянию равновесия. Однако это не противоречит утверждению о неустойчивости системы. Если считать , что все начальные состояния системы на фазовой плоскости равновероятны, то вероятность такого начального состояния, которое соответствует движению по направлению к особой точке, равна нулю. Поэтому всякое реальное движение будет удалять систему от состояния равновесия. Переходя обратно к координатам x,y, мы получим ту же качественную картину характера движения траекторий вокруг начала координат.
Пограничным между рассмотренными случаями узла и седла является случай, когда один из характеристических показателей, например λ 1 , обращается в нуль, что имеет место, когда определитель системы – выражение ad-bc=0 (см. формулу 4.8 ). В этом случае коэффициенты правых частей уравнений (4.4) пропорциональны друг другу :
и система имеет своими состояниями равновесия все точки прямой :
Остальные интегральные кривые представляют собой семейство параллельных прямых с угловым коэффициентом , по которым изображающие точки либо приближаются к состоянию равновесия, либо удаляются от него в зависимости от знака второго корня характеристического уравнения λ 2 = a+d. (Рис.4. 7 ) В этом случае координаты состояния равновесия зависят от начального значения переменных.
Корни λ 1 , λ 2 – комплексные сопряженные
В этом случае при действительных x и y мы будем иметь комплексные сопряженные ξ , η (4.10) . Однако, вводя еще одно промежуточное преобразование, можно и в этом случае свести рассмотрение к действительному линейному однородному преобразованию. Положим :
(4.16)
где a,b, и u,v – действительные величины. Можно показать, что преобразование от x,y к u,v является при наших предположениях действительным, линейным, однородным с детерминантом, отличным от нуля. В силу уравнений (4.10, 4.16) имеем :
откуда
(4.17)
Разделив второе из уравнений на первое , получим :
которое легче интегрируется , если перейти к полярной системе координат (r, φ ) . После подстановки получим , откуда :
.(4.18)
Таким образом, на фазовой плоскости u, v мы имеем дело с семейством логарифмических спиралей, каждая из которых имеет асимптотическую точку в начале координат. Особая точка, которая является асимптотической точкой всех интегральных кривых, имеющих вид спиралей , вложенных друг в друга, называется фокусом ( рис.4.8 ) .
Рассмотрим характер движения изображающей точки по фазовым траекториям. Умножая первое из уравнений (4.17) на u , а второе на v и складывая , получаем :
Где
Пусть a 1 < 0 (a 1 = Re λ ) . Изображающая точка тогда непрерывно приближается к началу координат, не достигая его в конечное время. Это означает, что фазовые траектории представляют собой скручивающиеся спирали и соответствуют затухающим колебаниям переменных. Это – устойчивый фокус .
В случае устойчивого фокуса, как и в случае устойчивого узла, выполнено не только условие Ляпунова, но и более жесткое требование. Именно, при любых начальных отклонениях система по прошествии времени вернется как угодно близко к положению равновесия. Такая устойчивость, при которой начальные отклонения не только не нарастают, но затухают, стремясь к нулю, называют абсолютной устойчивостью .
Если в формуле (4.18) a 1 >0 , то изображающая точка удаляется от начала координат, и мы имеем дело с неустойчивым фокусом . При переходе от плоскости u,v к фазовой плоскости x , y спирали также останутся спиралями, однако будут деформированы.
Рассмотрим теперь случай, когда
a
1
=0
. Фазовыми траекториями на плоскости
u, v
будут
окружности
которым на плоскости
x,y
соответствуют эллипсы
:
Таким образом, при a 1 =0 через особую точку x= 0, y= 0 не проходит ни одна интегральная кривая. Такая изолированная особая точка, вблизи которой интегральные кривые представляют собой замкнутые кривые, в частности, эллипсы, вложенные друг в друга и охватывающие особую точку, называется центром.
Таким образом, возможны шесть типов состояния равновесия в зависимости от характера корней характеристического уравнения (4.7). Вид фазовых траекторий на плоскости x, y для этих шести случаев изображен на рис. 4.9.
Рис. 4.9. Типы фазовых портретов в окрестности стационарного состояния для системы линейных уравнений (4.4).
Пять типов состояния равновесия грубые, их характер не изменяется при достаточно малых изменениях правых частей уравнений (4.4). При этом малыми должны быть изменения не только правых частей, но и их производных первого порядка. Шестое состояние равновесия – центр – негрубое. При малых изменениях параметров правой части уравнений он переходит в устойчивый или неустойчивый фокус.
Бифуркационная диаграмма
Введем обозначения:
.
(4.11)
Тогда характеристическое уравнение запишется в виде:
.
(4.12)
Рассмотрим плоскость с прямоугольными декартовыми координатами s , D и отметим на ней области, соответствующие тому или иному типу состояния равновесия, который определяется характером корней характеристического уравнения
.(4.13)
Условием устойчивости состояния равновесия будет наличие отрицательной действительной части у l 1 и l 2 . Необходимое и достаточное условие этого – выполнение неравенств s > 0, D > 0 . На диаграмме (4.15) этому условию соответствуют точки, расположенные в первой четверти плоскости параметров. Особая точка будет фокусом, если l 1 и l 2 комплексны. Этому условию соответствуют те точки плоскости, для которых , т.е. точки между двумя ветвями параболы s 2 = 4 D . Точки полуоси s = 0, D >0, соответствуют состояниям равновесия типа центр. Аналогично, l 1 и l 2 - действительны, но разных знаков, т.е. особая точка будет седлом, если D <0, и т.д. В итоге мы получим диаграмму разбиения плоскости параметров s , D , на области, соответствующие различным типам состояния равновесия.
Рис. 4.10. Бифуркационная диаграмма
для системы линейных уравнений 4.4
Если коэффициенты линейной системы a, b, c, d зависят от некоторого параметра, то при изменении этого параметра будут меняться и величины s , D . При переходе через границы характер фазового портрета качественно меняется. Поэтому такие границы называются бифуркационными – по разные стороны от границы система имеет два топологически различных фазовых портрета и, соответственно два разных типа поведения.
На диаграмме видно, как могут проходить такие изменения. Если исключить особые случаи – начало координат, – то легко видеть, что седло может переходить в узел, устойчивый или неустойчивый при пересечении оси ординат. Устойчивый узел может перейти либо в седло, либо в устойчивый фокус, и т.д. Отметим, что переходы устойчивый узел – устойчивый фокус и неустойчивый узел – неустойчивый фокус не являются бифуркационными, так как топология фазового пространства при этом не меняется. Более подробно мы поговорим о топологии фазового пространства и бифуркационных переходах в лекции 6.
При бифуркационных переходах меняется характер устойчивости особой точки. Например, устойчивый фокус через центр может переходить в неустойчивый фокус. Эта бифуркация называется бифуркацией Андронова-Хопфа по именам исследовавших ее ученых. При этой бифуркации в нелинейных системах происходит рождение предельного цикла, и система становится автоколебательной (см. лекцию 8).
Пример. Система линейных химических реакций
Вещество Х притекает извне с постоянной скоростью, превращается в вещество Y и со скоростью, пропорциональной концентрации вещества Y , выводится из сферы реакции. Все реакции имеют первый порядок, за исключением притока вещества извне, имеющего нулевой порядок. Схема реакций имеет вид:
(4.14)
и описывается системой уравнений:
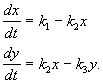(4.15)
Стационарные концентрации получим, приравняв правые части нулю:
.(4.16)
Рассмотрим фазовый портрет системы. Разделим второе уравнение системы (4.16) на первое. Получим:
.(4.17)
Уравнение (4.17) определяет поведение переменных на фазовой плоскости. Построим фазовый портрет этой системы. Сначала нарисуем главные изоклины на фазовой плоскости. Уравнение изоклины вертикальных касательных:
Уравнение изоклины горизонтальных касательных:
Особая точка (стационарное состояние) лежит на пересечении главных изоклин.
Теперь определим, под каким углом пересекаются координатные оси интегральными кривыми.
Если x= 0, то .
Таким образом, тангенс угла наклона касательной к интегральным кривым y=y(x), пересекающим ось ординат x=0 , отрицателен в верхней полуплоскости (вспомним, что переменные x, y имеют значения концентраций, и поэтому нас интересует только правый верхний квадрант фазовой плоскости). При этом величина тангенса угла наклона касательной увеличивается с удалением от начала координат.
Рассмотрим ось y= 0. В месте пересечения этой оси интегральными кривыми они описываются уравнением
При тангенс угла наклона интегральных кривых, пересекающих ось абсцисс, положителен и увеличивается от нуля до бесконечности с увеличением x .
При .
Затем при дальнейшем увеличении тангенс угла наклона уменьшается по абсолютной величине, оставаясь отрицательным и стремится к -1 при x ® ¥ . Зная направление касательных к интегральным кривым на главных изоклинах и на осях координат, легко построить всю картину фазовых траекторий.
 |
|
Характер устойчивости особой точки установим, пользуясь методом Ляпунова. Характеристический определитель системы имеет вид:
.
Раскрывая определитель, получим характеристическое уравнение системы: , т.е. корни характеристического уравнения оба отрицательны. Следовательно, стационарное состояние системы представляет собой устойчивый узел. При этом концентрация вещества X стремится к стационарному состоянию всегда монотонно, концентрация вещества Y может проходить через min или max. Колебательные режимы в такой системе невозможны.
Ряды Тейлора служат эффективным средством для изучения функций, аналитических в круге zol Для исследования функций, аналитических в кольцевой области, оказывается возможным построение разложений по положительным и отрицательным степеням (z - zq) вида обобщающим тейлоровские разложения. Ряд (1), понимаемый как сумма двух рядов называется рядом Лорана. Ясно, что областью сходимости ряда (1) является общая часть областей сходимости каждого из рядов (2). Найдем ее. Областью сходимости первого ряда является круг радиус которого определяется по формуле Коши-Адамара Внутри круга сходимости ряд (3) сходится к аналитической функции, причем в любом круге меньшего радиуса, он сходится абсолютно и равномерно. Второй ряд представляет собой степенной ряд относительно переменного Ряд (5) сходится внутри своего круга сходимости к аналитической функции комплексного переменного m-*oo причем в любом круге меньшего радиуса он сходится абсолютно и равномерно, ^го означает, что областью сходимости ряда (4) является внешность круга - Если то существует общая область сходимости рядов (3) и (4) - круговое кольцо в котором ряд (1) сходится к аналитической функции. При этом в любом кольце, он сходится абсолютно и равномерно. Пример 1. Определить область сходимости рада Ряды Лорана Изолированные особые точки и их классификация М Область сходи мости первого ряда - внешность круга а область с ходи мости второго ряда - внутренность круга Тем самым, данный ряд сходится в колы»о Теорема 15. Любую функцию f(z), однозначную и аполитичную в круговом котьце можно представить в этом кольце в виде суммы сходящегося ряда коэффициенты Сп которого определены однозначно и вычисляются по формулам где 7р - окружность радиуса м Зафиксируем внутри кольца Я произвольную точку z. Построим окружности центрами в точке го, радиусы которых удовлетворяют неравенствам и рассмотрим новое кольцо По интегральной теореме Коши для многосвязной области имеем Преобразуем отдельно каждый из интегралов в сумме (8). Для всех точек £ по окружности 7д* выполняется соотношение де суммы равномерно сходящегося ряда 1 1 Поэтому дробь ^ можно представить в ви- /" / Умножая обе части на непрерывную функцию (О и проводя почленное интегрирование вдоль окружности, получим, что Преобразование второго интеграла проведем несколько по-иному. Для всех точек £ на окружности ir> выполнено соотношение Поэтому дробь ^ можно представить в виде суммы равномерно сходящегося ряда Умножая обе части на непрерывную функцию) и интегрируя почленно вдоль окружности 7/, получи м, что Заметим, что подынтегральные функции в формулах (10) и (12) являются аналитическими функциями в круговом кольце. Поэтому в силу теоремы Коши значения соответствующих интегралов не изменятся, если заменить окружности 7/г и 7г/ любой окружностью. Это позволяет объединить формулы (10) и (12), Заменяя интегралы в правой части формулы (8) их выражениями (9) и (11) соответственно, получим нужное разложение Так как z - произвольная точка кольца, то отсюда следует, что ряд (14) сходится к функции f(z) всюду в этом кольце, причем в любом кольце ряд сходится к этой функции абсолютно и равномерно. Докажем теперь, что разложение вида (6) единственно. Предположим, что имеет место еще одно разложение Тогда всюду внутри кольца R будем иметь На окружности ряды (15) сходятся равномерно. Умножим обе части равенства (где т - фиксированное целое число, и проинтегрируем оба ряда почленно. В результате получим в левой части, а в правой - Сщ. Таким образом, (4, = Ст. Так как m - произвольное число, то последнее равенство доказывает единственность разложения. Ряд (6), коэффициенты которого вычисляются поформулам (7), называется рядом Лорана функции f(z) в кольце Совокупность членов этого ряда с неотрицательными степенями называется правильной частью ряда Лорана, а с отрицательными - его главной частью. Формулы (7) для коэффициентов ряда Лорана на практике применяются редко, ибо, как правило, требуют громоздких вычислений. Обычно, если это возможно, используются готовые тейлоровские разложения элементарных функций. На основании единственности разложения любой законный прием приводит к одному и тому же результату. Пример 2. Рассмотреть разложения в ряд Лорана функции различных областях, приняв Фуисция /(г) имеет две особые точки: . Следовательно, имеется три кольцевых области, с центром в точке го = 0. в каждой из которых функция /(г) является аналитической: а) круг кольцо внешность круга (рис.27). Найдем лорановские разложения функции /(z) в каждой из этих областей. Представим /(z) в виде суммы элементарных дробей а) Круг Преобразуем соотношение (16) следующим обра- Используя формулу для суммы членов геометрической прогрессии, получим Подставим найденные разложения в формулу (17): Это разложение является рядом Тейлора функции /(z). б) Кольцо для функции -г остается сходящимся в этом кольце, так как Ряд (19) для функции j^j при |z| > 1 расходится. Поэтому преобразуем функцию /(z) следующим образом: вновь применяя формулу (19), получим, что Этот ряд сходится для. Подставляя разложения (18) и (21) в соотношение (20), получим в) Внешность круга для функции -г при |z| > 2 расходится, а ряд (21) для функ- Представим функцию /(z) в следующем виде: /<*> Используя формулы (18) и (19), получим ИЛИ 1 Эгот пример показывает, что для одной и той же функции f(z) лорановское разложение, вообще говоря, имеет различный вид для разных колец. Пример 3. Найти разложение 8 ряд Лорана функции Ряды Лорана Изолированные особые точки и их классификация а кольцевой области А Воспользуемся представлением функции f(z) в следующем виде: и преобразуем второе слагаемое Используя формулу для суммы членов геометричесхой прогрессии, получим Подставляя найденные выражения в формулу (22), имеем Пример 4. Разложить в ряд Лорана функцию в окреслюсти тонки zq = 0. Для любою комплексного имеем Положим Это разложение справедливо для любой точки z Ф 0. В данном случае кольцевая область представляет собой всю комплексную плоскость с одной выброшенной точкой z - 0. Эту область можно определить следующим соотношением: Данная функция является аналитической в области Из формул (13) для коэффициентов ряда Лорана такими же рассуждениями, что и в предыдущем параграфе, можно получить неравенства Kouiw. если функция f(z) ограничена на окружности, где М - постоянная),то Изолированные особые точки Точка zo называется изолированной особой точкой функции / (z), если существует кольцевая окрестность точки (это множество иногда называют также проколотой окрестностью точки 2о), в которой функция f(z) однозначна и аналитична. В самой точке zo функция либо не определена, либо не является однозначной и аналитичной. В зависимости от поведения функции /(г) при приближении к точке zo различаются три типа особых точек. Изолированная особая точка называется: 1) устранимой, если существует конечный 2) пмюсач, если 3) существенно особой точкой, если функция f(z) не имеет предела при Тип изолированной особой точки тесно связан с характером лорановского разложения функции выколотым центром го. Теорема 16. Изолированная особая точка z0 функции f(z) является устранимой особой точкой в том и только в тач случае, когда лорановское разложение функции f(z) в окрестности точки zo не содержит главной части, т. е. имеет вид Пусть zo - устранимая особая точка. Тогда существует конечный, следо- вательно, функция f(z) ограничена впрокологой окрестности точки го, Положим В силу неравенств Коши Так как р моямо выбрать скольугодно малым, то все коэффициенты при отрицательных степенях (z - 20) равны нулю: Обратно, пусть лорановское разложение функции /(г) в окрестности точки zq содержит только правильную часть, т. е. имеет вид (23) и, следовательно, является тейлоровским. Нетрудно видеть, что при z -* z0 У фуниции /(г) существует предельное значение: Теорема 17. Изолированная особая точка zq функции f(z) является устранимой тогда и только тогда, когда функция J(z) ограничена в некоторой проколотой окрестности точки zq, Згмечаи не. Пусть го - устранимая особая точка функции /(г). Полагая мы получим, чтофункция /(г) аналитична в некотором к руге с центром в точке го. Это определяет название точки - устранимая. Теорема 18. Изолированная особая точка zq функции f(z) является полюсом в том и только в том случае, когда главная частьлорановскогоразложения функции f(z) в окрестности точки содержит конечное (и положительное) числоотличных от нуля членов, т. е. имеет вид 4 Пусть z0 - полюс. Так как то существует проколотая окрестность точки z0, в которой функция f(z) аналитична и отлична от нуля. Тогда в этой окрестности определена аналитическая функция причем Следовательно, точка zq является устранимой особой точкой (нулем) функции или где h(z) - аналитическая функция, h(z0) Ф 0. Тогда аналитична и h(zo) ф 0, то функция щ аналитична в окрестности точки zq, и следовательно, откуда получаем, что Предположим теперь, что функция f(z) имеет в проколотой окрестности точки zо разложение вида (24). Это означает, что в этой окрестности функция f(z) аналитична вместе с функцией. Для функции g(z) справедливо разложение из которого видно, что zq - устранимая особая точка функции g(z) и существует Тогда функция при 0 стремится - полюс функции Имеет место еще один простой факт. Точка Zq - полюс функции f{z) в том и только в том случае, когда функцию g(z) = ущ можно доопределить до аналитической функции в окрестности точки zq, положив g(z0) = 0. Порядком полюса функции f(z) называется порядок нуля функции jfa. Из теорем 16 и 18 вытекает следующее утверждение. Теорема 19. Изолированная особая тонка является существенно особой в том и только в том случае, когда главная часть лорановского разложения в проколотой окрестности этой точки содержит бесконечно много отличных от нуля членов. Пример 5. Особой точкой функции является zo = 0. Имеем Ряды Лорана Изолированные особые точки и их классификация Следовательно, zo = О - устранимая особая точка. Разложение функции /(z) в ряд Лорана в окрестности нулевой точки содержит только правильную часть: Пример7. /(г) = Особая точка функции f(z) есть zq = 0. Рассмотрим поведение этой функции на действительной и мнимой осях: на действительной оси при х 0, на мнимой оси Следовательно, ни конечного, ни бесконечного предела f(z) при z -* 0 не существ ует. Значит, точка го = 0 - существенно особая точка функции f(z). Найдем лорановское разложение функции f(z) в окрестности нулевой точки. Для любого комплексного С имеем Положим. Тогда Лорановское разложение содержит бесконечное число членов с отрицательными степенями z.
Основные понятия и определения:
Нулем аналитической функции f(z) называется точка “a”, для которой f(a)=0.
Нулем порядка “n” функции f(z) называется точка «а», если но fn(a)¹0.
Особая точка «a» называется изолированной особой точкой функции f(z), если существует окрестность этой точки, в которой нет особых точек, кроме «a».
Изолированные особые точки бывают трех типов: .
1 устранимые особые точки;
3 существенно особые точки.
Тип особой точки может быть определен исходя из поведения данной функции в найденной особой точке, а также из вида ряда Лорана, полученного для функции в окрестности найденной особой точки.
Определение типа особой точки по поведению функции в ней.
1.Устранимые особые точки .
Изолированная особая точка a функции f(z) называется устранимой, если существует конечный предел .
2.Полюсы.
Изолированная особая точка a функции f(z) называется полюсом, если 
.
3.Существенно особые точки.
Изолированная особая точка a функции f(z) называется существенно особой точкой, если не существует ни конечный, ни бесконечный .
Между нулями и полюсами функции имеет место следующая связь.
Для того, чтобы точка a была полюсом порядка n функции f(Z), необходимо и достаточно, чтобы эта точка была нулем порядка n для функции .
Если n=1 полюс называется простым.
Определение: Изолированная особая точка однозначного характера называется:
а) устранимой, если главная часть разложения отсутствует;
б) полюсом, если главная часть содержит конечное число членов;
в) существенно особой точкой, если главная часть содержит бесконечное число членов.
а) Таким образом, в окрестности устранимой особой точки разложение имеет вид:
оно выражает функцию во всех точках круга |z-a| В центре z=a равенство неверно, т.к. функция при z=a имеет разрыв, а правая часть непрерывна. Если в центре значение функции изменить, приняв его равным значению правой части, то разрыв будет устранен- отсюда и название – устранимый. б) В окрестности полюса порядка m разложение в ряд Лорана имеет вид: в) В окрестности простого полюса Вычеты и формулы для их вычисления.
Вычетом аналитической функции f(z) в изолированной особой точке z 0 называется комплексное число, равное значению интеграла Обозначается вычет функции f(z) в изолированной особой точке z 0 символом Res f(z 0) или Res (f(z); z 0). Таким образом, Res f(z 0)= Если в формуле (22.15.1) положить n=-1, то получим: C -1 = или Res f(z 0)= C -1 , т.е. вычет функции f(z) относительно особой точки z 0 равен коэффициенту при первом члене с отрицательным показателем в разложении функции f(z) в ряд Лорана. Вычисление вычетов.
Правильные или устранимые особые точки. Очевидно, если z=z 0 есть правильная или устранимая особая точка функции f(z), то Res f(z 0)=0 (в разложении Лорана в этих случаях отсутствует главная часть, поэтому c-1=0). Полюс. Пусть точка z 0 является простым полюсом функции f(z). Тогда ряд Лорана для функции f(z) в окрестности точки z 0 имеет вид: Отсюда Поэтому, переходя в этом равенстве к пределу при z --z 0 , получаем Res f(z0)= Существенно особая точка. Если точка z 0 - существенно особая точка функции f(z), то для вычисления вычета функции в этой точке обычно непосредственно определяют коэффициент c-1 в разложении функции в ряд Лорана. Классификация событий. Сумма, произведение событий, их свойства, графическое представление.
События делятся на: 1. Случайные 2. Достоверные 3. Невозможные Достоверное – это такое событие, которое наступает обязательно в данных условиях (за ночью следует утро). Случайное – это такое событие, которое может произойти, а может и не произойти (сдача экзамена). Невозможное – это такое событие, которое в данных условиях не наступит (достать зеленый карандаш из коробки только с красными). Особая точка
в математике. 1) Особая точка кривой, заданной уравнением F (x, у
) = 0, - точка М 0 (х 0 , y 0
), в которой обе частные производные функции F (x, у
) обращаются в нуль: Если при этом не все вторые частные производные функции F (x, у
) в точке М 0 равны нулю, то О. т. называют двойной. Если наряду с обращением в нуль первых производных в точке М 0 обращаются в нуль и все вторые производные, но не все третьи производные равны нулю, то О. т. называется тройной, и т.д. При исследовании строения кривой вблизи двойной О. т. важную роль играет знак выражения Если Δ > 0, то О. т. называется изолированной; например, у кривой у 2 - х 4 + 4x 2
= 0 начало координат есть изолированная О. т. (см. рис. 1
). Если Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4
= 0 начало координат есть узловая О. т. (см. рис. 2
). Если Δ = 0, то О. т. кривой является либо изолированной, либо характеризуется тем, что различные ветви кривой имеют в этой точке общую касательную, например: а) точка возврата 1-го рода - различные ветви кривой расположены по разные стороны от общей касательной и образуют остриё, как у кривой у 2 - х 3
= 0 (см. рис. 3
, a
); б) точка возврата 2-го рода - различные ветви кривой расположены по одну сторону от общей касательной, как у кривой
(у - x 2
) 2 - х 5
= 0 (см. рис.
3
, б); в) точка самоприкосновения (для кривой у 2 - х 4
= 0 начало координат является точкой самоприкосновения; (см. рис. 3
, в). Наряду с указанными О. т. имеется много других О. т. со специальными названиями; например, асимптотическая точка - вершина спирали с бесконечным числом витков (см. рис. 4
), точка прекращения, угловая точка и т.д. 2) Особая точка дифференциального уравнения - точка, в которой одновременно обращаются в нуль и числитель и знаменатель правой части дифференциального уравнения (См. Дифференциальные уравнения) где Р и Q - непрерывно дифференцируемые функции. Предполагая О. т. расположенной в начале координат и используя Тейлора формулу (См. Тейлора формула), можно представить уравнение (1) в виде где P 1 (x, у
) и Q 1 (x, у
)- бесконечно малые по отношению к Именно, если λ 1 ≠ λ 2 и λ 1 λ 2 > 0 или λ 1 = λ 2 , то О. т. есть узел; все интегральные кривые, проходящие через точки достаточно малой окрестности узла, входят в него. Если λ 1 ≠ λ 2 и λ 1 λ 2 i β, α ≠ 0 и β ≠ 0, то О. т. есть фокус; все интегральные кривые, проходящие через точки достаточно малой окрестности фокуса, представляют собой спирали с бесконечным числом витков в любой сколь угодно малой окрестности фокуса. Если, наконец, λ 1,2 = ± i
β, β ≠ 0, то характер О. т. не определяется одними линейными членами в разложениях Р (х, у
) и Q (x, у
), как это имело место во всех перечисленных случаях; здесь О. т. может быть фокусом или центром, а может иметь и более сложный характер. В окрестности центра все интегральные кривые являются замкнутыми и содержат центр внутри себя. Так, например, точка (0, 0) является узлом для уравнений у
" = 2у/х
(λ 1 = 1, λ 2 = 2; см. рис. 5
, а) и y
" = у/х
(λ 1 = λ 2 = 1; см. рис. 5
, б), седлом для уравнения у" = -у/х
(λ 1 = -1, λ 2 = 1; см. рис. 6
), фокусом для уравнения у" =
(х + у
) /
(х - у
) (λ 1 = 1 - i
, λ 2 = 1 + i
; см. рис. 7
) и центром для уравнения у" = -x / y
(λ 1 = -i
, λ 2 = i
; см. рис. 8
). Если х, у) и Q (х, у
) аналитические, окрестность О. т. высшего порядка может распадаться на области: D 1 - заполненные интегральными кривыми, обоими концами входящими в О. т. (эллиптические области), D 2 - заполненные интегральными кривыми, одним концом входящими в О. т. (параболические области), и D 3 - области, ограниченные двумя интегральными кривыми, входящими в О. т., между которыми расположены интегральные кривые типа гипербол (гиперболические области) (см. рис. 9
). Если нет интегральных кривых, входящих в О. т., то О. т. называется точкой устойчивого типа. Окрестность устойчивой О. т. состоит из замкнутых интегральных кривых, содержащих О. т. внутри себя, между которыми расположены спирали (см. рис. 10
). Изучение О. т. дифференциальных уравнений, т. е. по существу изучение поведения семейств интегральных кривых в окрестности О. т., составляет один из разделов качественной теории дифференциальных уравнений и играет важную роль в приложениях, в частности в вопросах устойчивости движения (работы А. М. Ляпунов а, А. Пуанкаре и др.). 3) Особая точка однозначной аналитической функции - точка, в которой нарушается аналитичность функции (см. Аналитические функции). Если существует окрестность О. т. a
, свободная от других О. т., то точку а
называют изолированной О. т. Если а
- изолированная О. т. и существует конечный a называют устранимой О. т. Путём надлежащего изменения определения функции в точке а (или доопределения её в этой точке, если функция в ней вообще не определена), именно, полагая f
(a
) = b
, можно добиться того, что a
станет обыкновенной точкой исправленной функции. Например, точка z
= 0 является устранимой О. т. для функции f 1 (z
) = f
(z
), если z
≠ 0, и f
1 (0), = 1, точка z
= 0 является обыкновенной точкой [f
1 (z
) аналитична в точке z
= 0]. Если а
- изолированная О. т. и а называют полюсом или несущественно особой точкой функции f
(z
), если же Лорана ряд) функции f
(z
) в окрестности изолированной О. т. не содержит отрицательных степеней z - а
, если а
- устранимая О. т., содержит конечное число отрицательных степеней z - а
, если а
- полюс (при этом порядок полюса р
определяется как наивысшая степень а - существенно особая точка. Например, для функции точка z
= 0 является полюсом порядка р
, для функции точка z
= 0 является существенно особой точкой. На границе круга сходимости степенного ряда должна находиться по крайней мере одна О. т. функции, представляемой внутри этого круга данным степенным рядом. Все граничные точки области существования однозначной аналитической функции (естественной границы) являются О. т. этой функции. Так, все точки единичного круга | z
| = 1 являются особыми для функции Для многозначной аналитической функции понятие «О. т.» более сложно. Помимо О. т., в отдельных листах римановой поверхности функции (то есть О. т. однозначных аналитических элементов) всякая точка ветвления также является О. т. функции. Изолированные точки ветвления римановой поверхности (то есть такие точки ветвления, что в некоторой их окрестности ни в одном листе нет других О. т. функции) классифицируются следующим образом. Если а - изолированная точка ветвления конечного порядка и существует конечный а называют критическим полюсом. Если а
- изолированная точка ветвления бесконечного порядка и а называют трансцендентной О. т. Все остальные изолированные точки ветвления называют критическими существенно особыми точками. Примеры: точка z
= 0 является обыкновенной критической точкой функции f (z
) = ln z
и критической существенно особой точкой функции f
(z
) = sin ln z
. Всякая О. т., кроме устранимой, является препятствием при аналитическом продолжении, т. е. аналитическое продолжение вдоль кривой, проходящей через неустранимую О. т., невозможно. Большая советская энциклопедия. - М.: Советская энциклопедия
.
1969-1978
.
Указывает сюда. См. также особая точка (дифференциальные уравнения). Особенность или сингулярность в математике это точка, в которой математический объект (обычно функция) не определён или имеет нерегулярное поведение (например, точка в которой… … Википедия
Аналитической функции точка, в к рой нарушаются условия аналитичности. Если аналитическаяфункция f(z)задана в нек рой окрестности точки z0 всюду … Физическая энциклопедия
Аналитической функции точка, в которой нарушается аналитичность функции … Большой Энциклопедический словарь
особая точка
- — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN singular point … Справочник технического переводчика
1) О. т. аналитической функции f(z) препятствие для аналитического продолжения элемента функции f(z) комплексного переменного zвдоль какого либо пути на плоскости этого переменного. Пусть аналитическая функция f(z) определена некоторым… … Математическая энциклопедия
Аналитической функции, точка, в которой нарушается аналитичность функции. * * * ОСОБАЯ ТОЧКА ОСОБАЯ ТОЧКА аналитической функции, точка, в которой нарушается аналитичность функции … Энциклопедический словарь
особая точка
- ypatingasis taškas statusas T sritis automatika atitikmenys: angl. singular point vok. singulärer Punkt, m rus. особая точка, f pranc. point particulier, m; point singulier, m … Automatikos terminų žodynas
, взятого в положительном направлении по окружности L с центром в точке z 0 , лежащей в области аналитичности функции f(z) (т.е. в кольце 0<|z-z0| . (22.15.1)
p = 2, 3, …)
Смотреть что такое "Особая точка" в других словарях:
